


(OK, I know I just turned off all but the geeks)
Exponential smoothing is a technique where the more recent data is weighted more heavily when computing an 'average'. It's the
computer equivalent of putting "X"s by players' names in the program when they're hot. Think how a player's whole-season
average may not be the best measure of his ability today.
Say I'm looking at a game where I've rated all the players. Now
the game goes off and Player A wins. I'm obviously going to increase his rating and decrease the ratings of the other players. But, by how much? With exponential smoothing, I can give him a new rating which rates recent performances more heavily, for example:
New Rating = (0.9 x Old Rating) + (0.1 x This Game Performance)
The coefficients always total 1.0 (in this example). The lower value (0.1) is the smoothing constant, typically called "Alpha". The value (size) of Alpha determines how fast the rating reacts to current (i.e., this game ) performance. In my studies, I vary the value of Alpha to see which value (responsiveness) give me the best results.
- Too high, and the model reacts very quickly - too quickly, in fact, and it is what statisticians call 'nervous'
- Too low, and the model is not very responsive to new data
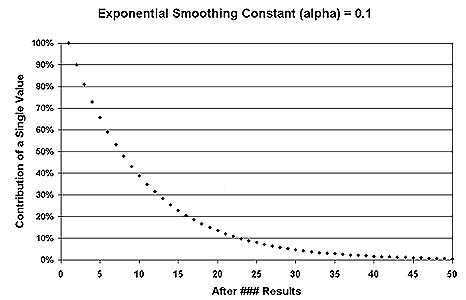
The above graph illustrates (for an Alpha value of 0.1) the
diminishing significance of historical data over time.
In my system, the average player rating is 125. 1,000 is 'Perfect'. Early-gamers are typically in the 50-150 range, late-gamers 100-200. The high and low extremes are rare.
So (for the geeks that are still reading), do you use such a technique?
